[kata][python] 택시 기하학에서의 원 넓이 구하기

유클리드 기하학과 택시 기하학에서의 원 넓이 구하기

출처: 백준 알고리즘 3053번 문제

원의 반지름 R을 입력으로 받아서,

유클리드 기하학에서의 원의 넓이와 택시 기하학에서의 원의 넓이를 출력하라.

소수점 6자리까지만 출력

입력
    1

출력
    3.141593
    2.000000 

택시 기하학에 대해서는 따로 찾아보는게 훨씬 이해가 쉽겠지만,

스스로 정리도 할겸 우선 간략하게 설명을 하고 들어가도록 하겠다.

유클리드 기하학에서의 두 지점의 거리는 좌표평면상의 최단거리를 의미한다.

하지만 실제 도시에서 두 지점의 거리는 좌표평면상의 최단거리와 다르다.

택시가 한 지점에서 다른 지점으로 이동하는 것을 상상해보자.

택시는 건물을 뚫고 지나가지 못하기때문에 좌회전도하고 우회전도한다.

구불구불 굽어진 길을 가다보면 어느새 목적지에 도착하는데,

이 때 출발지점 T1(x1, y1)과 도착지점 T2(x2, y2) 사이의 거리를 구하는 공식은 다음과 같다.

공식을 깊이 이해할 필요는 없다.

원리만 생각해보자.

모눈종이 위에 임의의 점 T1, T2를 찍어 놓았다고 상상해보자.

그리고 T1에서 T2로 가기 위한 방법을 생각해보자.

모눈종이를 가로질러서 직선을 긋는게 가장 빠르겠지만 (유클리드 거리).

모눈종이에 그어져있는 선만 따라서 이동할 수 있다고 가정하자.

그럼 다음과 같은 경로들이 가능할 것이다.

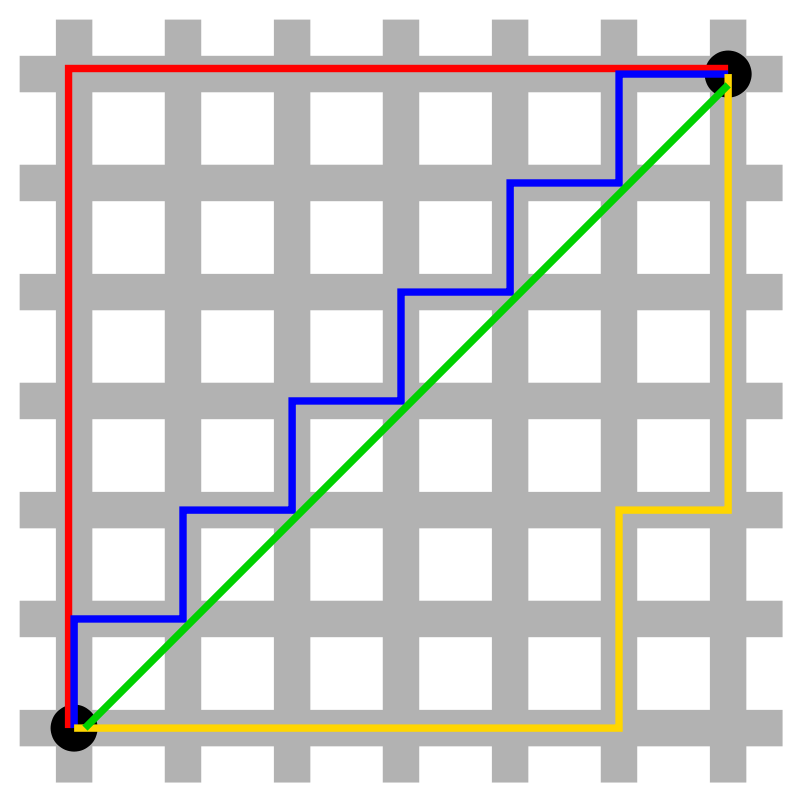
그림출처: 위키백과

이 때, 모눈종이를 가로지르는 초록색 선이 유클리드 거리이자 최단거리이다.

하지만 모눈종이의 선만 따라 이동할 수 있다고 했으므로, 이 경우는 제외하자.

그리고 나머지 빨간색, 파란색, 노란색 선은 모두 거리가 12로 같다.

위에서 적었던 공식은 그냥 이 거리를 구하는 공식이다.

빨간색 선의 세로길이를 보면 y2 - y1이다.

빨간색 선의 가로길이를 보면 x2 - x1이다.

즉, 총 길이는 이 둘을 합한 (y2 - y1) + (x2 - x1) 이다.

이걸 좀 더 일반적으로 정리한게 앞에서 언급한 |x1 - x2| + |y1 - y2| 인 것이다.

그럼, 택시 기하학에서의 원은 어떤 모양일까?

원이란 ‘평면상의 어떤 점에서 거리가 일정한 점들의 집합’이다.

거리가 일정하므로, 유클리드 기하학에서의 원은 우리가 흔히 알고있는 동그라미 모양이다.

하지만 택시 기하학에서의 원은 좀 다르다.

한 점에서 택시 기하학적 거리가 같은 모든 점을 그려 연결하면 다음과 같은 마름모 꼴이 나온다.

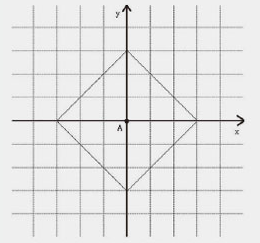
그림출처: 조선pub

조금 혼란스러울수도 있는데,

원점부터 선만 따라서 마름모를 이루는 각 점에 도착하는 거리를 재보면 3으로 모두 같다는것을 알 수 있다.

그리고 이 원의 반지름 또한 3이다.

원점에서 (3, 0)과 (0, 3) 까지 닿는 길이를 생각해보자.

즉, 택시 기하학에서의 반지름이 R인 원의 넓이란,

“두 대각선의 길이가 2R인 마름모의 넓이” 와 같다.

마름모의 넓이는 한 대각선(2R)에서 다른 대각선을 2등분한 길이(R)를 곱해주면 된다.

즉, 택시 기하학에서 반지름이 R인 원의 넓이는 2R² 이다.

여기까지 이해됐으면 이제 코드를 짜는건 아주 간단하다.

내 풀이

  1 import sys
  2 import math
  3
  4 R = int(sys.stdin.readline())
  5
  6 print("{0:.6f}".format(math.pi * (R ** 2)))
  7 print("{0:.6f}".format(2 * (R ** 2)))

2번째 라인에서 정확한 pi값을 구하기 위한 math 함수를 import했다.

4번째 라인에서 반지름 R을 입력받았다.

5번째 라인에서 유클리드 기하학에서의 원의 넓이인 pi 곱하기 R² 을 출력했다.

6번째 라인에서는 택시 기하학에서의 원의 넓이인 2 곱하기 R² 을 출력했다.

다른사람 풀이

  1 a = int(input())
  2 print('%.6f' % (3.14159265358979323846264338327950288*a*a))
  3 print('%.6f' % (2*a*a))

math 모듈을 사용하는대신 pi값을 직접 입력해 유클리드 기하학 원 넓이를 구했다.

택시 기하학 원 넓이는 나와 동일하게 구했다.

분석

사실 이번 알고리즘은 요구사항에 있는 택시 기하학 자체를 이해하는게 핵심이었던 문제라서,

코드레벨에서 보면 거의 다 똑같이 구현했다.

나는 택시 기하학의 개념을 처음 접해서 배경지식을 공부하는데 시간이 좀 걸렸는데,

미리 알고있던 사람은 30초도 안걸려 쉽게 해결할 수 있는 문제였다.

만약 유클리드 기하학의 원의 넓이를 구하는 방법도 몰랐다면 완성시간은 훨씬 더 늘어났을 것이다.

평소에 꾸준히 공부하며 배경지식을 쌓는것도 중요한 것 같다.

코딩장이

-장이: [접사] ‘그것과 관련된 기술을 가진 사람’의 뜻을 더하는 접미사.

Share Share